Yax2+bx+c What Is B
By the definition of.
Yax2+bx+c what is b. What is the vertex of y=x 2 +4x+3?. Consider the graph of the equation y=ax^2+bx+c, when a does not equal 0. In a straight line, the standard form of the equation is ax + by = c where:.
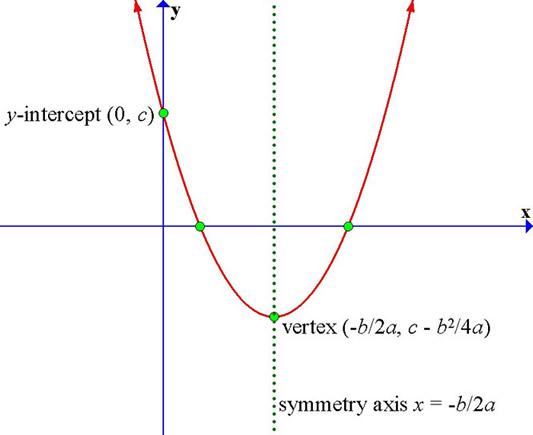
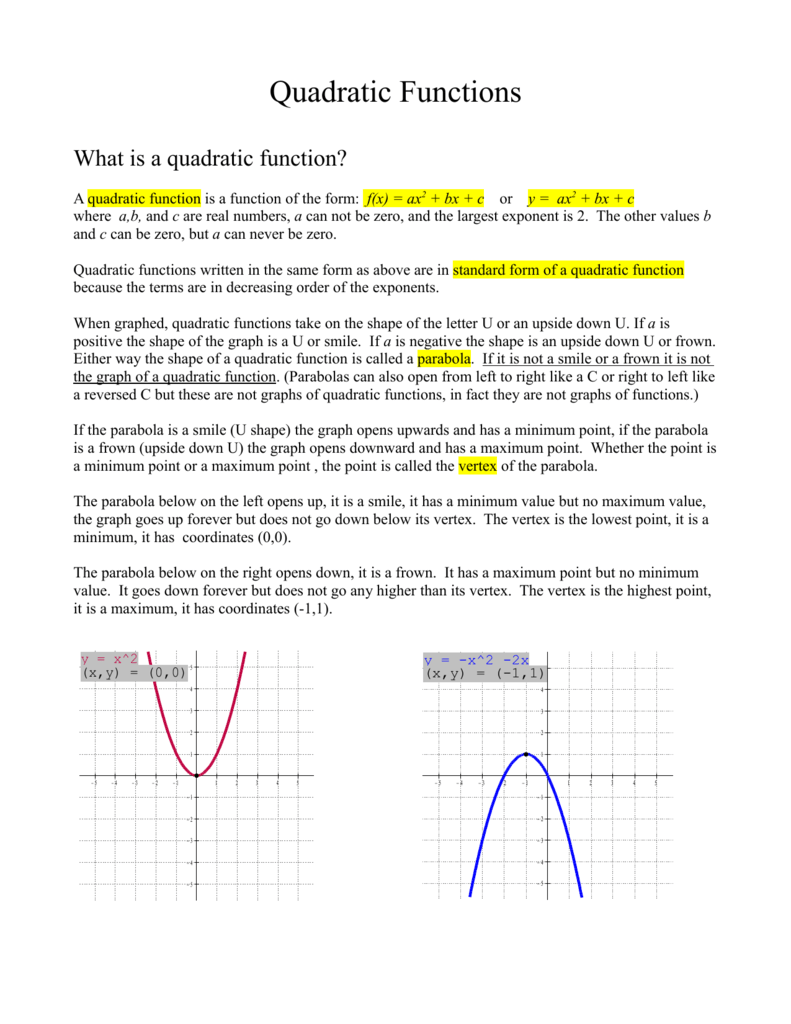
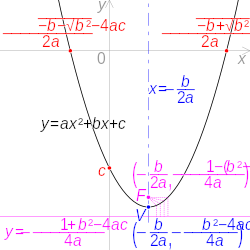
8.2 Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function y = mx + b, where the highest power of x is 1, is a straight line. M is the slope. If we have the equation y=ax 2 +bx+c, how can we can find the x-coordinate of the vertex?.
Well the thing is, even if a and c are given. So solving ax 2 + bx + c = 0 for x means, among other things, that you are trying to find x-intercepts.Since there were two solutions for x 2 + 3x – 4 = 0, there must then be two x-intercepts on the graph.Graphing, we get the curve below:. The exception to it not being used as a vertex is when the b is equal to 0.
Answer choices (2,1) (-2,1) (0,0) (-2,-1) s:. On solving for y,. The form ax 2 + bx + c = 0 is called standard form of a quadratic equation.
Move the loose number over to the other side. I'm pretty sure c is the y-intercept, and I think b is used to partially calculate the turning point. New questions in Mathematics.
So as long as b^2 - 4ac is greater than 0. ( 5 is obtained as half the width.) => 10 = - k(5)^2 => k = - 2/5. Most of us are aware that the quadratic equation yields the graph of a parabola.
A negative B goes from high to low and a positive B goes from low to high. $$3x^{2}-2x-8$$ We can see that c (-8) is negative which means that m and n does not have the same sign. Solve for x y=ax^2+bx+c.
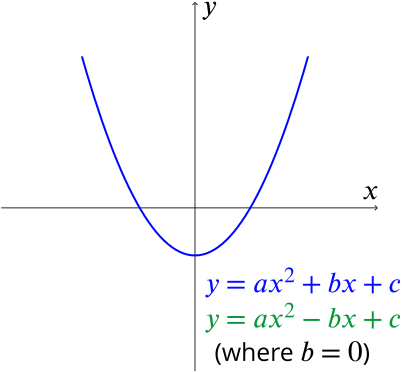
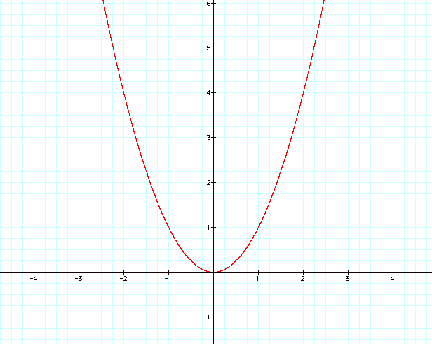
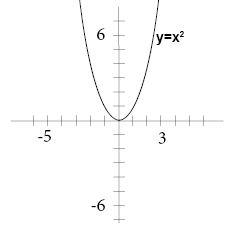
But I'm not sure. Rewrite the equation as. The simplest quadratic relation of the form y=ax^2+bx+c is y=x^2, with a=1, b=0, and c=0, so this relation is graphed first.
The c is always a constant. Putting this value of b in the above two equations and solving them together, we get a = 3, b= 6 and c= -5. Since (1,0) is on the graph, c = 1.
Its equation with repect to its vertex at origin is of the form. For each point, give a linear equation in a, b, and c. This is Introduction to. Hi Debbie, The point here is that you can only add quantities that have the same units.
Remember, the standard form of a quadratic looks like ax 2 +bx+c, where 'x' is a variable and 'a', 'b', and 'c' are constant coefficients;. Since (-3,10) is on the graph, 9a - 3b + c = 10. Find the quadratic function y=ax^2+bx+c whose graph passes through the given points:.
In general, the function y = ax2 + bx + c, where a, b, and c are constants and a ≠ 0, is called a quadratic function.For instance, y = 2x2 + 3x + 4, y = x 2 – 3, and y = –x – 6x + 1 are quadratic functions y of x. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. We multiply quantities of different units (eg.
4a + 2b = 14. The intercept is (0,-p). Plots of quadratic function y = ax 2 + bx + c, varying each coefficient separately while the other coefficients are fixed (at values a = 1, b = 0, c = 0) A quadratic equation with real or complex coefficients has two solutions, called roots.
In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third. X =-b ± b 2-4 a c 2 a. Find the quadratic function which takes the value 41 at x=-2 and the value at x=5 and is minimized at x=21 Y=Ax^2 - Bx + C Algebra -> Quadratic Equations and Parabolas -> SOLUTION:.
Find the quadratic function which takes the value 41 at x=-2 and the value at x=5 and is minimized at x=21 Y=Ax^2 - Bx + C Log On. Y = ax 2 + bx + c. (-1,6), (1,4), (2,9) Expert Answer Substituting in the points you get the following equations 6 = a (-1)^2 + b (-1) + c 6 = a - b + c 4 = a(1)^2 + b(1) + c 4 = a + b + c 9 = a(2)^2 + b(2) + c 9 = 4a + 2b view the full answer.
Since (2,15) is on the graph, 4a + 2b + c = 15. How to Find the y Intercept y = ax2 + bx + c The y intercept is a number that is not generally used as a vertex, it is used as one of the places to plot the line. In other words, both sides of the given equation need to be differentiated thrice.
Y = a(x-p) 2 + p because of the vertex being (h,k) = (p,p) To find a, we use the other condition. So in this case:. When b is more negative, the vertex moves down, and the axis of symmetry moves to the right.
` ` `y=ax^2 + bx +c`is the original function for a parabola. Unless you give us an answer to what that polynomial equals. It’s formula is (0, c).
3a - b = 3. Explorations of the graph. Given this equation, what is the value of a + b + c?.
The correct answer is 9. Y = 3x^2 + 6x - 5. Factor out whatever is multiplied on the squared term.
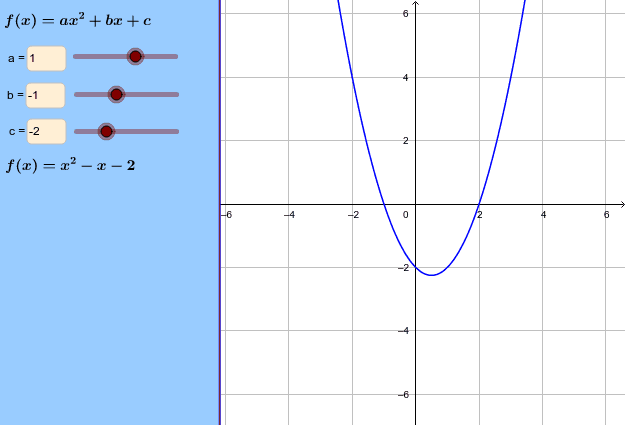
Find an answer to your question what is y = (x-6)^2 - 2 in y = ax^2+bx+c form A partial proof was constructed given that MNOP is a parallelogram. You can change the shape and location of this by increasing the a, b, and c values. B can be:-b +/- squareroot(b^2 - 4ac) / 2a.
MATLAB ® displays a warning message if A is badly scaled or nearly singular, but performs the calculation regardless. Find the equation of the parabola, y = ax^2 +bx + c , that passes through the points (-1, 6), (1, 4), and (2, 9). Before solving a quadratic equation using the Quadratic Formula, it's vital that you be sure the equation is in this form.
Substitute the values , , and into the quadratic formula and solve for. X(2x + 3) – 2(x – 3) = ax 2 + bx + c;. Y = ax + b, formula to calculate the a and b is:.
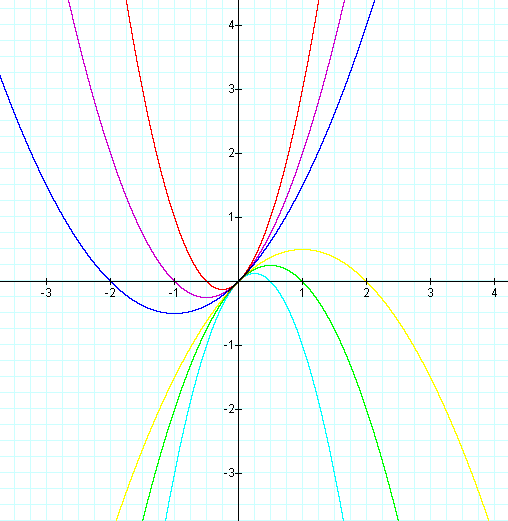
I suppose you want an inverted parabola which opens downwards. (1) y = x² - 2x + 1 (2) y = x² + 1 (3) y = x² + 2x + 1 In the image below, Equation (1) is the black parabola, Equation (2) is green, and Equation (3) is red. B can be ANYTHING.
What is the value of a eadair21 is waiting for your help. Plug those values in to the equation y = x^2 + x + c and you'll get the same equation as you've been given. X = A\B solves the system of linear equations A*x = B.The matrices A and B must have the same number of rows.
Y – c = ax 2 + bx:. The parabolic form of the equation which is y =a(x-h) 2 + k transforms into. Since there are three constants mathA/math, mathB/math, mathC/math involved, the differential equation should be of third order (not necessarily linear).
When you substitute, you get a = -(2/p) So the. Where a, b, and c are real numbers, and a!=0. Mean of y x i:.
Parabolas The graph of a quadratic equation in two variables (y = ax2 + bx + c) is called a parabola. The parabola y=ax^2+bx+c has vertex (p,p) and y-intercept (0,-p), where p≠ 0. When a coefficient is missing in front of a variable, you know that it's just equal to 1 :).
,If the sum of their reciprocal is 2/5 ( Quadratic equation) Algebra. The slope of a straight line -- that number -- indicates the rate at which the value of y changes with respect to the value of x. The general equation for a parabola is y = ax 2 + bx + c, where a, b, c are constants.
If a, b, and c are integers, 6x 2 + cx + 6 = (ax + 2)(bx + 3) for all values of x, and 1 < a < b, what is the value of c?. Interactive lesson on the graph of y = ax² + bx + c, including its axis of symmetry and vertex, and rewriting the equation in vertex form. XXxTenTacion Jul 16, 18.
Let's examine three parabolas in which a and c remain constant and only b changes. Y = - kx^2. B can be any number.
The ith number of x. Find the value of \(y\) when \(x=6\). If there is only one explanatory variable, it is called simple linear regression, the formula of a simple regression is y = ax + b, also called the line of best fit of dataset x and dataset y.
For any quadratic equation of the form y = ax 2 + bx + c, the quadratic formula below. Given a quadratic equation y = ax^2 + bx + c, (i) What is the effect of changing the value of the number c on the parabola?. If Y = Ax^2 + Bx +C is the position of the car the velocity is the derivative of this equation the velocity is the slope of the 1st equation dy/dx = v = 2Ax +B.
Now put theses values of a, b, c in eq.(1), it gives the required quadratic equation as :. Add your answer and earn points. What are the units of each constant if y and x are in meters?.
To get foot-pounds) and divde quantities of. The graphs of quadratic relations are called parabolas. This equation can also be factored to the form:`y.
B is the coefficient of the x term. $$\begin{align} y &= ax^2 + bx + c \\0.3 cm 4 &= a(3)^2 + b(3) + c \\0.3 cm 4 &= a(9) + 3b + c \\0.3 cm 4 &= 9a + 3b + c \end{align} $$ Now, we have three equations with three unknowns. I'm dealing with quadratic equations (y=ax2+bx+c) and I need to know what the three variables, a, b and c stand for.
Y = ax 2 + bx + c:. 5) C is the constant that tells you how far up or down the graph moves. They are where the graph crosses the x-axis, or simply put, where y = 0.
Make room on the left-hand side, and put a copy of "a" in front of this space. A is the coefficient of the x^2 term. QUADRATIC RELATION A quadratic relation in two variables is a relation that can be written in the form.
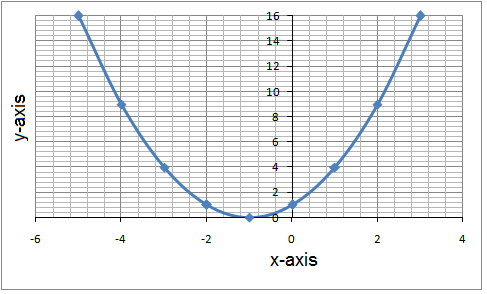
The vertex of this parabola is \((2,3)\) and the parabola contains the point \((4,4)\). Y = ax 2 + bx + c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 + bx + c, where a, b, and c are rational numbers. Use the quadratic formula to find the solutions.
Divide the first equation by 3 and the second by 2:. Distribute and simplify the expressions on the left to match the quadratic on. The parabola represented by the polynomial expression of the form {eq}\displaystyle y=ax^2+bx+c=0;a,b,c\in C {/eq} is called a quadratic expression.
Mean of x y:. So in the format y = ax^2 + bx + c a, b and c are the coefficents of the x^2 term, the x term and the constant term (without x). Therefore, since the variables x and y are the coördinates of any point on that line, that equation is the equation of a straight line with slope a and y-intercept b.Which is what we wanted to prove.
What is the solution set of xlx>-5) xlx <5)?. Move to the left side of the equation by subtracting it from both sides. A is the coefficient of the x term b is the coefficient of the y term c is the constant term the slope-intercept form of the equation of a straight line is y = mx + b where:.
We now want to find m and n and we know that the product of m and n is -8 and the sum of m and n multiplied by a (3) is b (-2) which means that we're looking for two factors of -24 whose sum is -2 and we also know that one of them is positive and of them is negative. The following graphs are two typical parabolas their x-intercepts are marked by red dots, their y-intercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot:. (5 points) A) 3x^2 + y^2 + 12x - 7 = 0 B) 3x^2 + 3y^2 + 12x - 7 = 0 C) 3x^2 + y + 12x - 7 = Algebra.
38,407 results, page 9 Maths. (A) The Vertex is 3 units above the vertex of the original. What is (a, b, c)?.
Y = ax + b. Suppose the function shown below was expressed in standard form y=ax^2+bx+c. 4) B is the slope of the equation.
If you don't, you might use the wrong values for a, b, or c, and then the formula will give incorrect solutions. If a is multiplied by 3, what is true of the graph of the resulting parabola?. The sum of two numbers is 40.we need to find the no.
Since c = 1, we then have 9a - 3b = 9. The roots of a quadratic function are the same as its zeroes. Suppose that we have an equation y=ax^2+bx+c whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0).
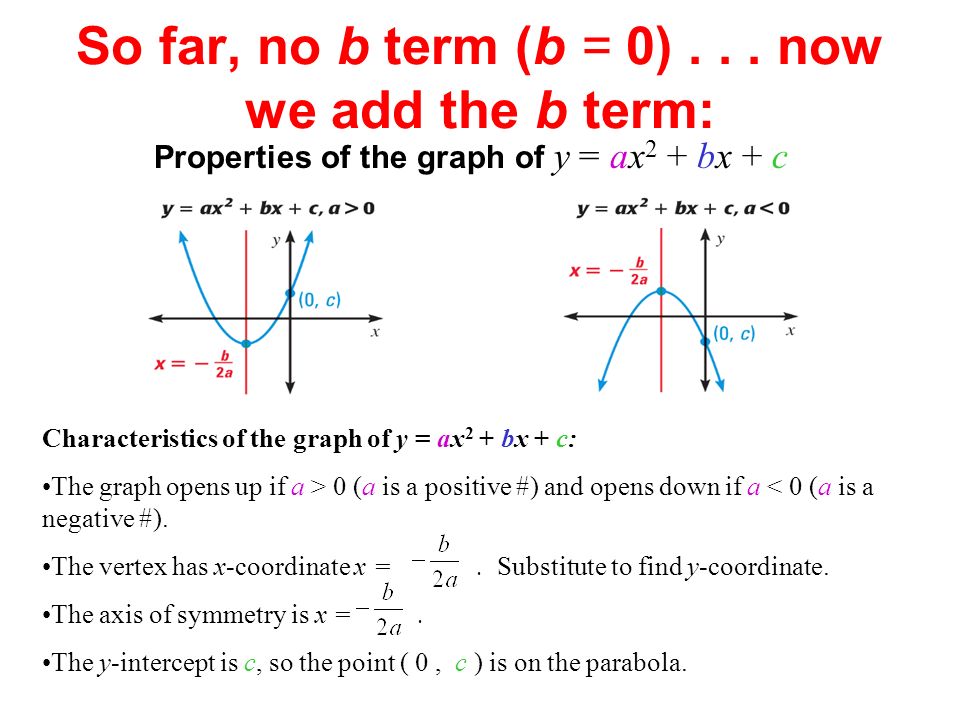
We are going to explore how each of the variables a, b, and c affect the graph of .First, let's take a look at the simplest of the quadratic equation , where a = 1, b = 0, and c = 0. The graph of y = ax^2 + bx + c A nonlinear function that can be written on the standard form a x 2 + b x + c, w h e r e a ≠ 0 is called a quadratic function. The graph of \(y=ax^2 + bx + c\) is a parabola with vertical axis of symmetry.
We have split it up into three parts:. A, b, c in the quadratic equation are constants and real numbers. Knowing 'a', 'b', and 'c' helps you solve quadratic equations!.
A quadratic function can have 0, 1, or 2 roots. Will find the roots, or zeroes, of the equation. As its width is 10, and height 10, a point (5, 10) is on the parabola.
By Kristina Dunbar, UGA. The numbers between -5 and 5 the empty set all numbers except -5 and 5 all real numbers. This gives us the quadratic equation.
If there is no constant, then the origin lies at 0. Suppose you have ax 2 + bx + c = y, and you are told to plug zero in for y.The corresponding x-values are the x-intercepts of the graph.

Solved In Y Ax 2 Bx C The X Coordinate Of The Verte Chegg Com

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
Equations And Graphs
Yax2+bx+c What Is B のギャラリー
Solution Discriminating Quadratics Underground Mathematics
If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community
Q Tbn 3aand9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau

Unique Quadratic Equation In The Form Y Ax 2 Bx C
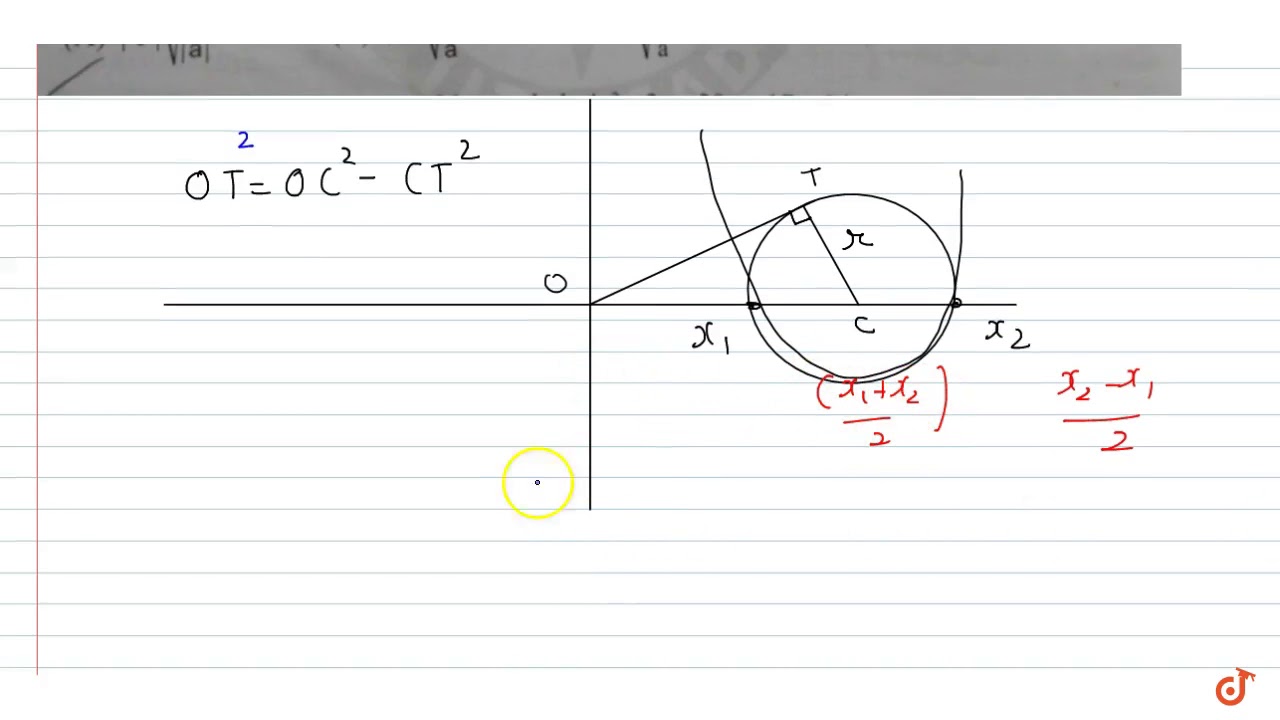
A Parabola Y Ax 2 Bx C Ac Gt 0 Crosses The X Axis At A And B A Variable Circle Is Dra Youtube
Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download

Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download

The Expression Y Ax 2 Bx C Has Always The Same Sign As Of A If A 4ac Lt B 2 B 4ac Youtube
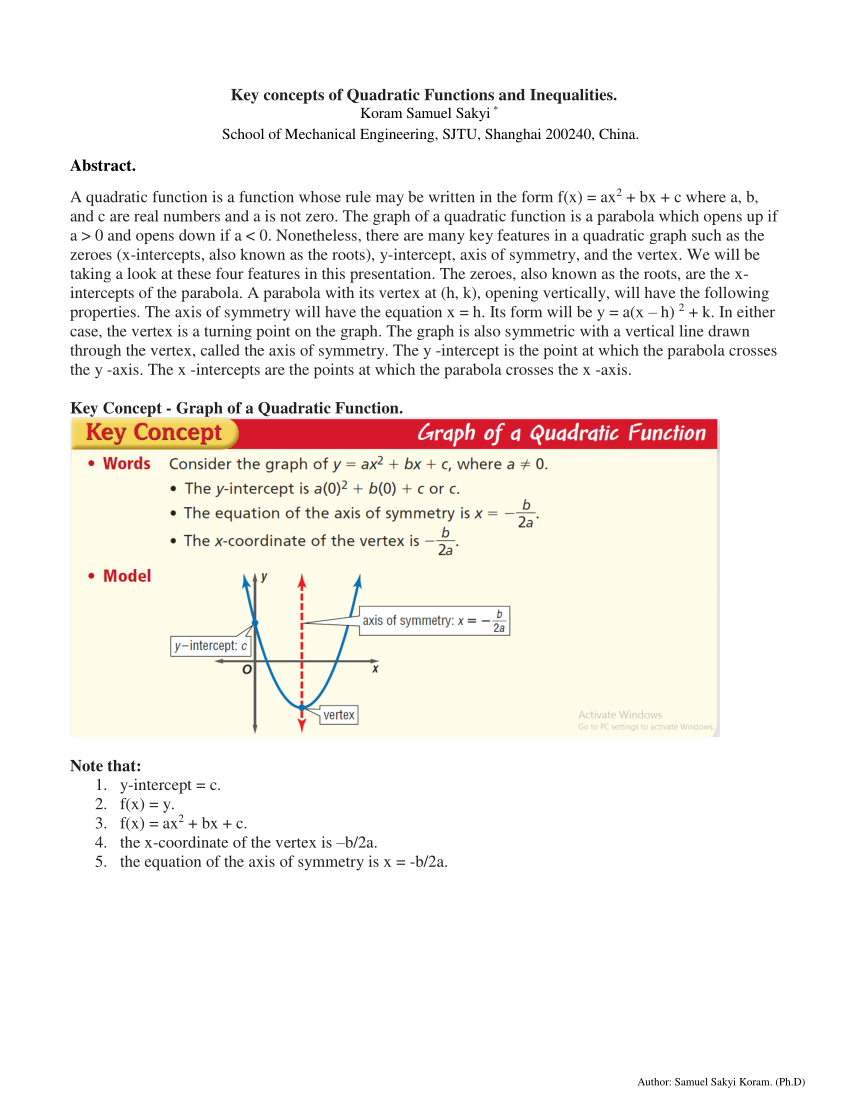
Pdf Key Concepts Of Quadratic Functions And Inequalities First Edition
Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola

Solved Use The Graph Of Y Ax2 Bx C To Solve A Quadr Chegg Com

Writing Equation Of A Quadratic Number Pattern By Finding A B And C Of Y Ax 2 Bx C Youtube

Aim Review Of Parabolas Graphing Do Now Write Down The Standard Equation Of A Parabola Answer Y Ax 2 Bx C Homework Workbook Pg 427 Part Ppt Download

2 Graph Of Y Ax 2 Bx K Graph Of Y Mx K Download Scientific Diagram

The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
Exploring Parabolas Y Ax 2 Bx C
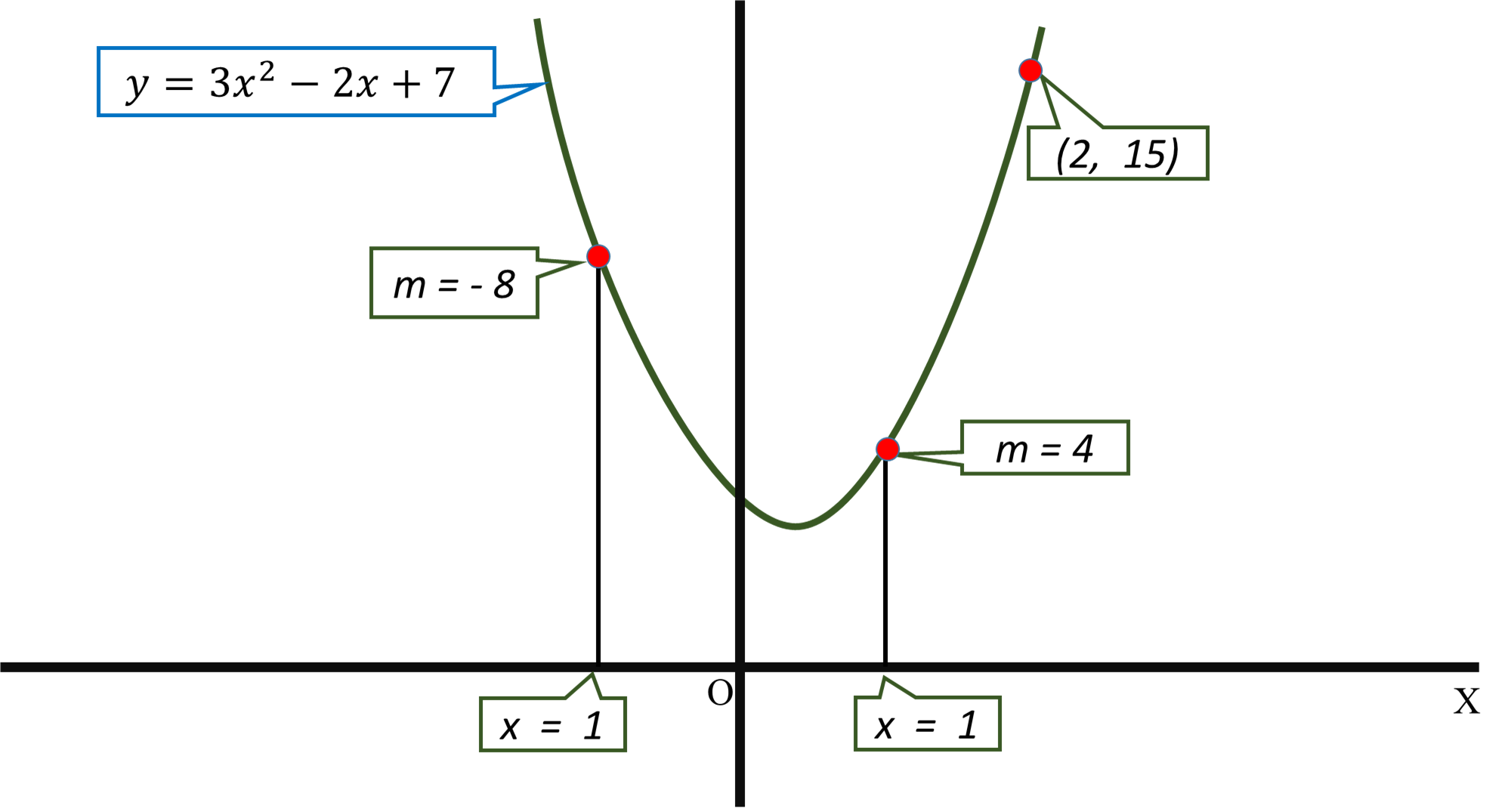
How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic
Examining The Parabola Assignment 2
Quadratic Functions
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora

Quadratic Graph Example Y Ax Expii
Solution Draw A Sketch Graph Of Y Ax 2 Bx C If A Lt 0 B Lt 0 C Lt 0 Discriminant 0
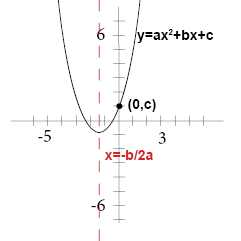
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
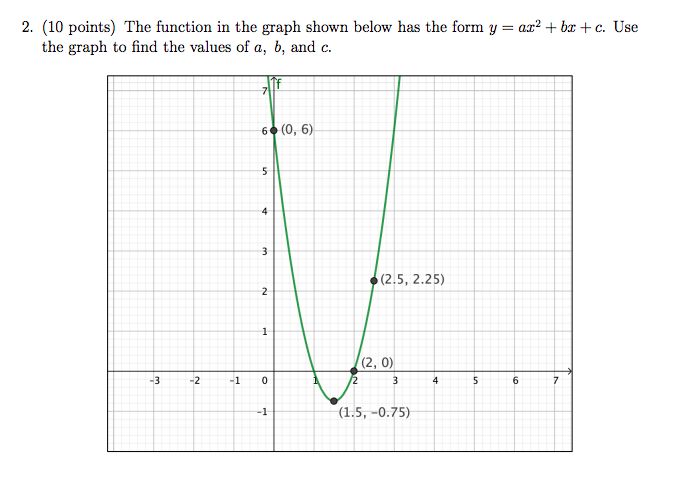
Solved 2 10 Points The Function In The Graph Shown Bel Chegg Com
Precalculus Section 1 7 Define And Graph Quadratic Functions Any Function That Can Be Written In The Form Y Ax 2 Bx C Is Called A Quadratic Function Ppt Download
The Following Figure Shows The Graph Of F X Ax 2 Bx C Then

Activity Sheet On Understanding How B Affects The Graph Of Y Ax 2 Bx C Activity Sheets Graphing Activities

Solved The Equation For A Parabola Has The Form Y Ax 2 Chegg Com
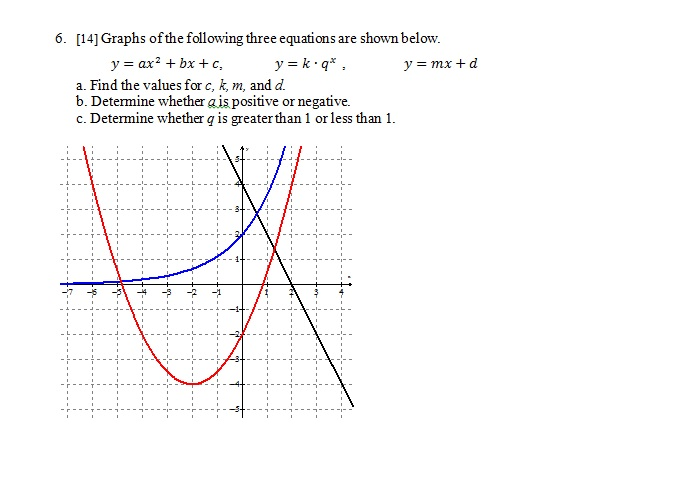
Solved Graphs Of The Following Three Equations Are Shown Chegg Com

Graphing Y Ax 2 Bx C
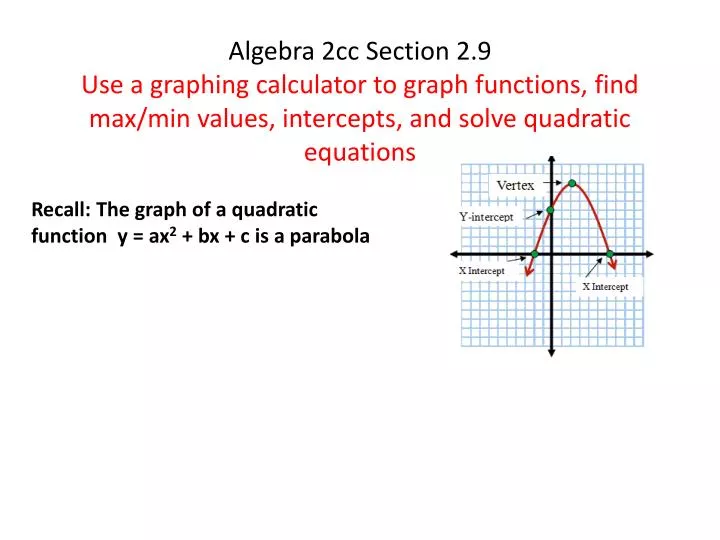
Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id
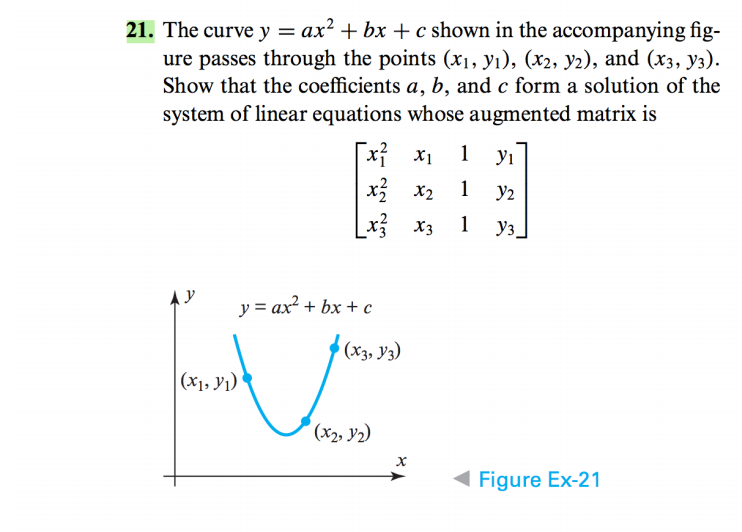
Solved The Curve Y Ax 2 Bx C Shown In The Accompany Chegg Com
Linear Algebra Webnotes Class Assignments Chapter 1
If Ax Bx C 0 And A B C 0 What Would Be The Value S Of X Quora
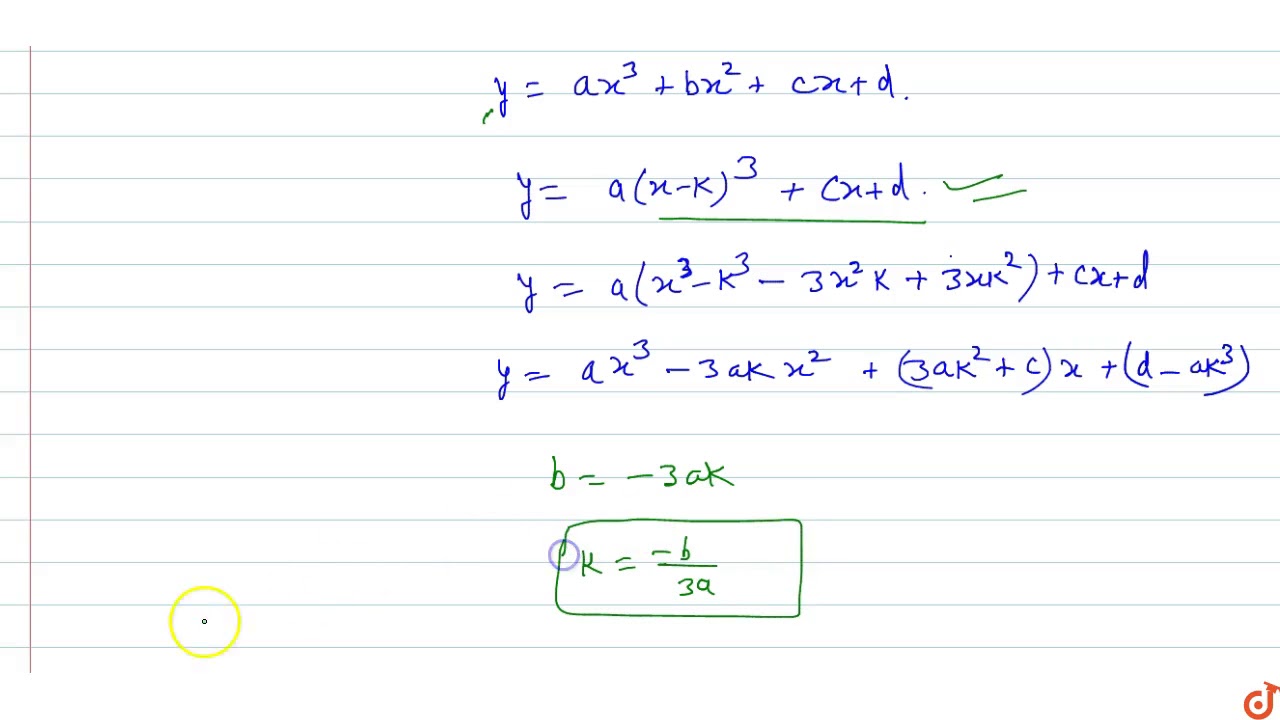
If The Graph Of Y Ax 3 Bx 2 Cx D Is Symmetric About The Line X K Then The Value Of A K Youtube

B Value Definition Explanation Video Lesson Transcript Study Com
Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Sarthaks Econnect Largest Online Education Community

Quadratic Function

Quadratic Function Wikipedia

Ch8 Quadratic Equation Solving Methods General Form Of Quadratic Equation Ax 2 Bx C 0 A Quadratic Equation X 2 7x 10 0a B Ppt Download
Quadratic Function Wikipedia
Linear Algebra Webnotes Class Assignments Chapter 1

Math Spoken Here About Quadratics 3

Graphing Quadratics

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com

If The Diagram In Fig 2 22 Shows The Graph Of The Polynomial F X Ax Bx C Then A A Gt 0 Brainly In
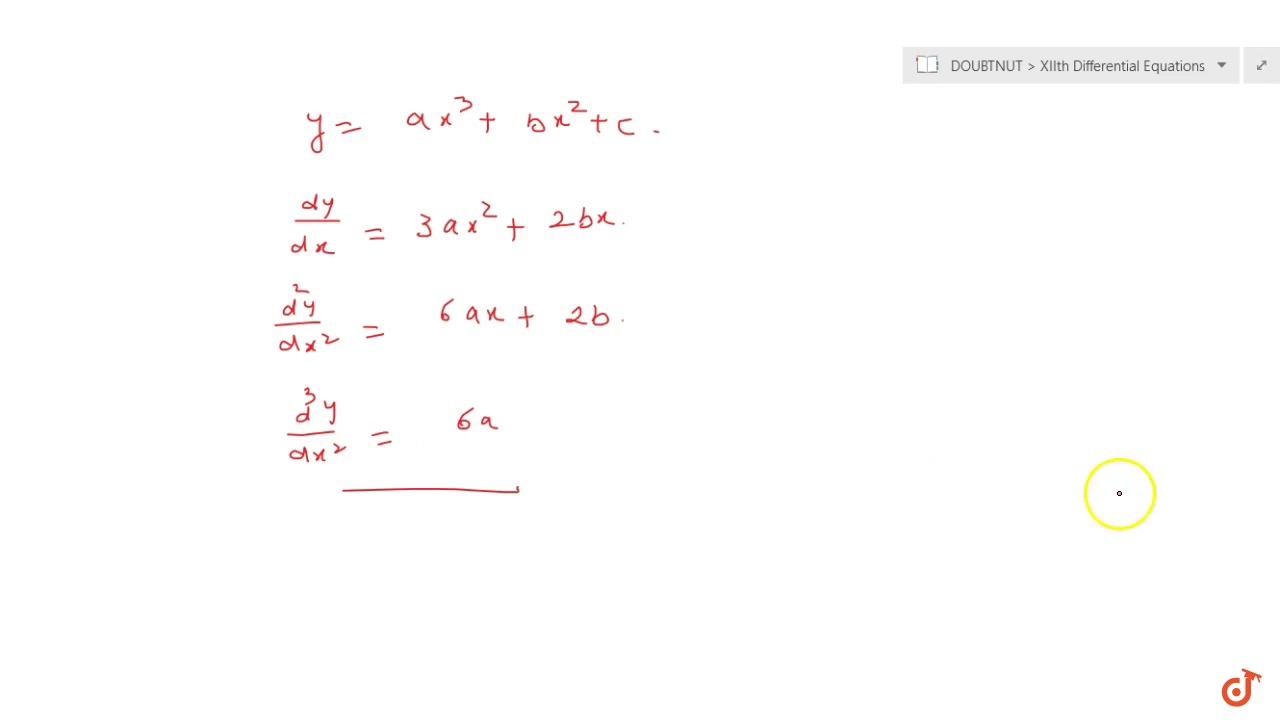
Show That Y A X 3 B X 2 C Is A Solution Of The Differential Equation D 3y Dx 3 6a Youtube

Quadratic Function Wikiwand

Math Forum Ask Dr Math

0101 Graphing Quadratic Functions
The Graph Of Y Ax 2 Bx C Geogebra
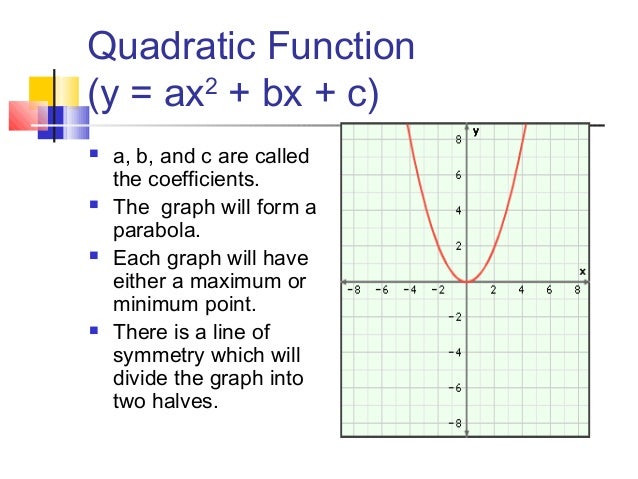
5 1 Quadratic Functions

Quadratic Equation Wikipedia
Q Tbn 3aand9gcsoxi Ejbyqsmv0q0mpk0drfxs9e4wo7 Nazdmw7dnnjqm3wzk Usqp Cau
Q Tbn 3aand9gcrj4zefjn32tclwxwszidmmbulqtnieycx Jyr6u1jhn9b002k8 Usqp Cau

Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange

Graphing Y Ax2 Bx C Youtube

Quadratic Formula Wikipedia
The Quadratic Function
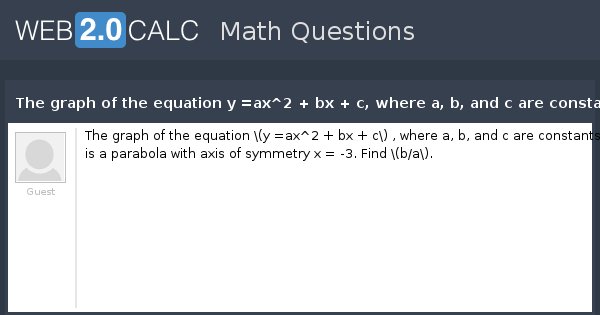
View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A
Quadratic Relations Y Ax 2 Bx C Between The A N B P And Download Scientific Diagram
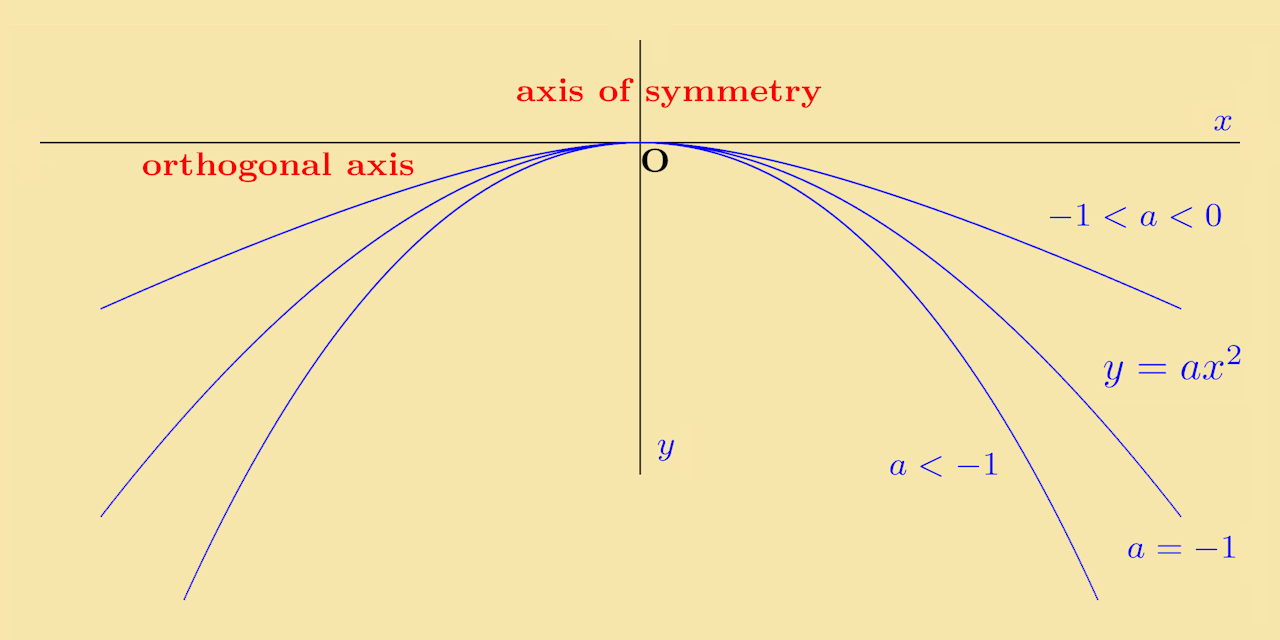
Pplato Basic Mathematics Quadratic Functions And Their Graphs
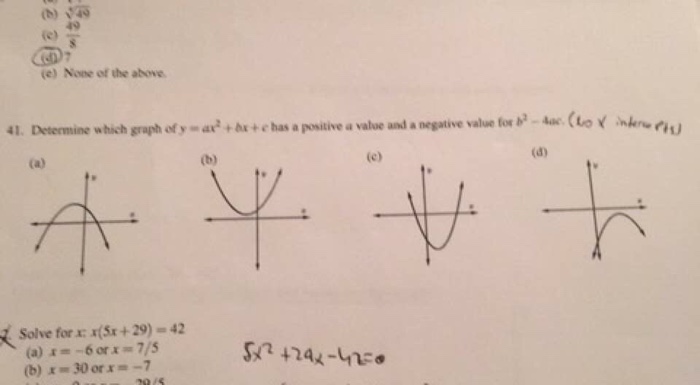
Solved Determine Which Graph Of Y Ax 2 Bx C Has A P Chegg Com
Observations Of Asymptotic Behavior

Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download
Examining The Parabola Assignment 2
Exploring Parabolas Y Ax 2 Bx C

Unique Quadratic Equation In The Form Y Ax 2 Bx C
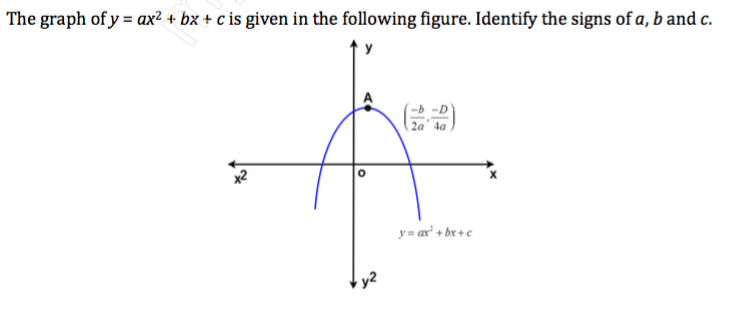
Solved The Graph Of Y Ax 2 Bx C Is Given In The Fol Chegg Com
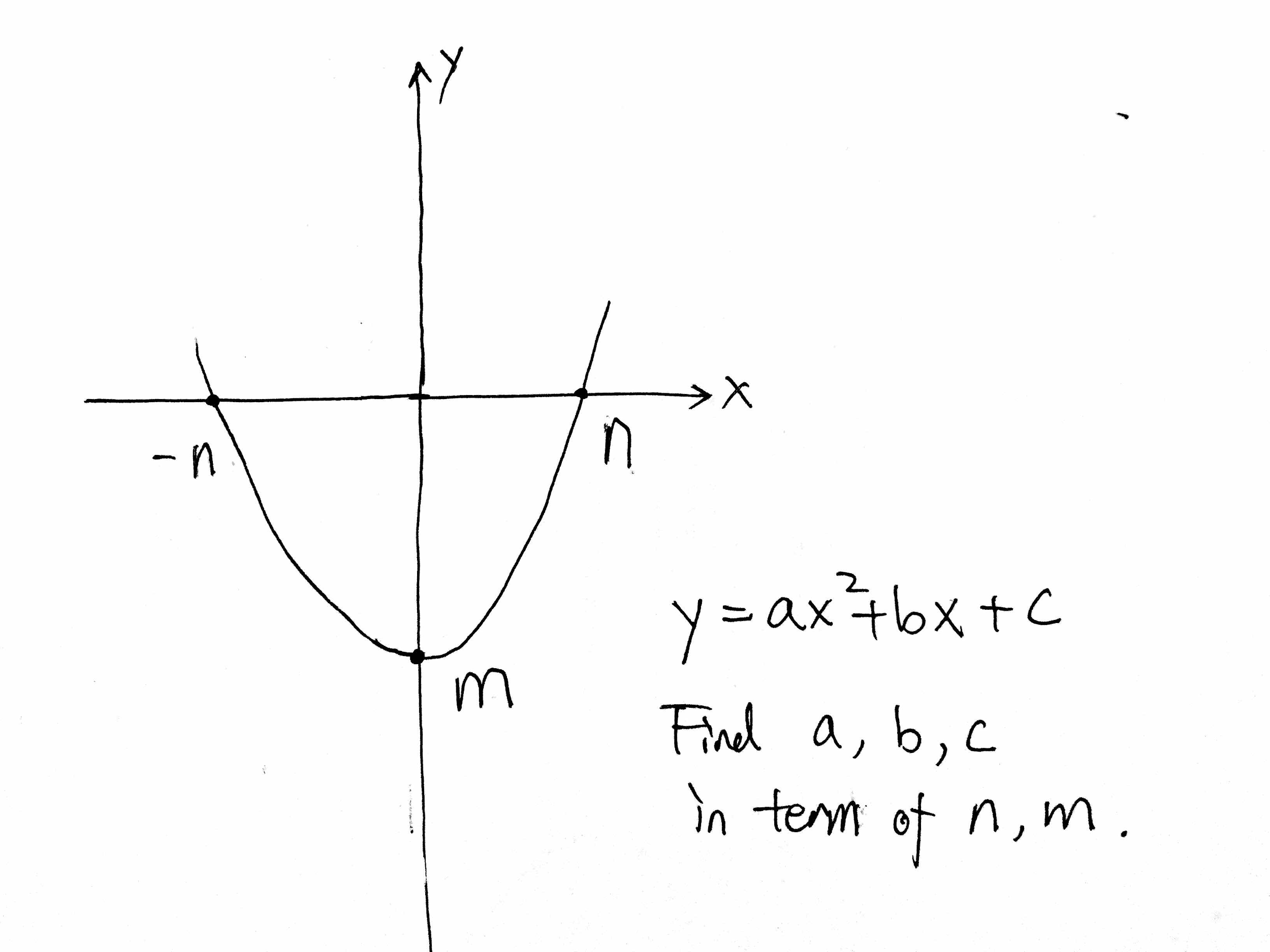
Solved Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com

The Adjoining Figure Shows The Graph Of Y Ax 2 Bx C Then Youtube

The Graphs Of Y Ax 2 Bx C Are Given In Figure Identify The Signs Of A B And C In Each Of The Following

Quadratic Formula Calculator

Quadratic Equation Wikipedia
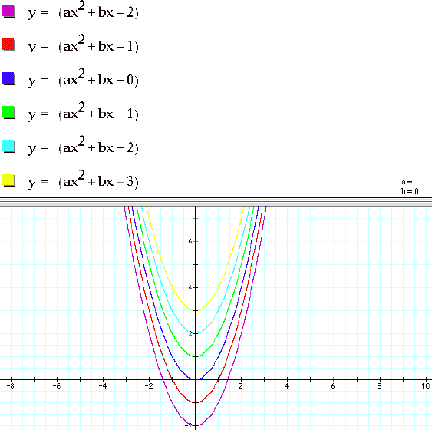
Assignment 2

Quadratic Function

Analyzing Properties Of Parabolas Name

Solved A Quadratic Equation In The Form Y Ax 2 Bx C Chegg Com

Graphing Quadratic Functions Ppt Download
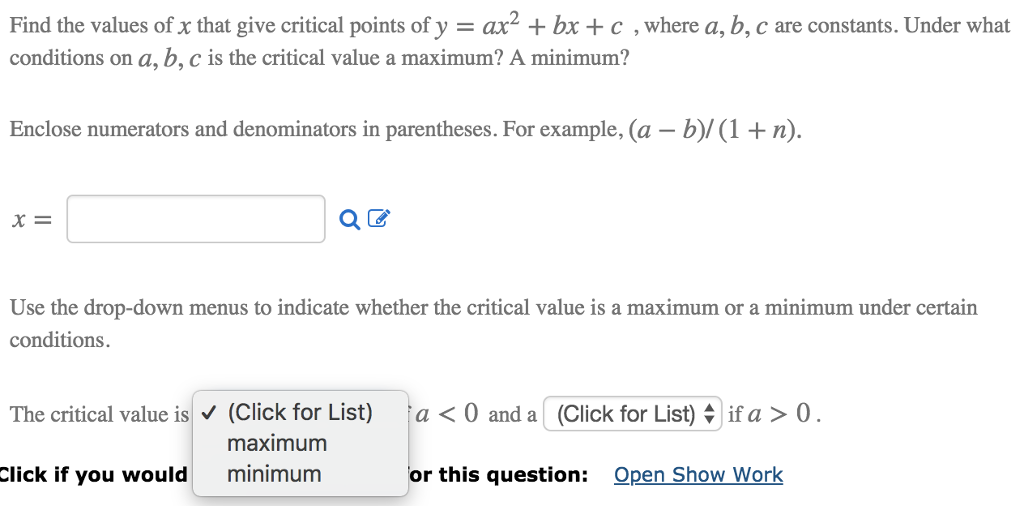
Solved Find The Values Of X That Give Critical Points Of Chegg Com
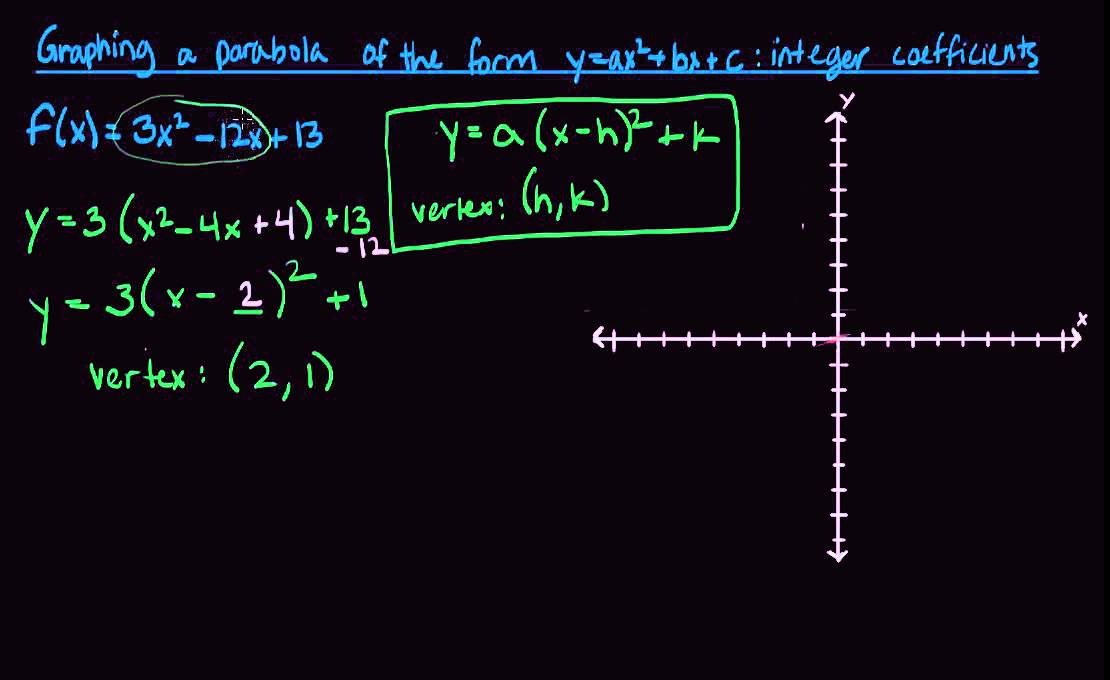
Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
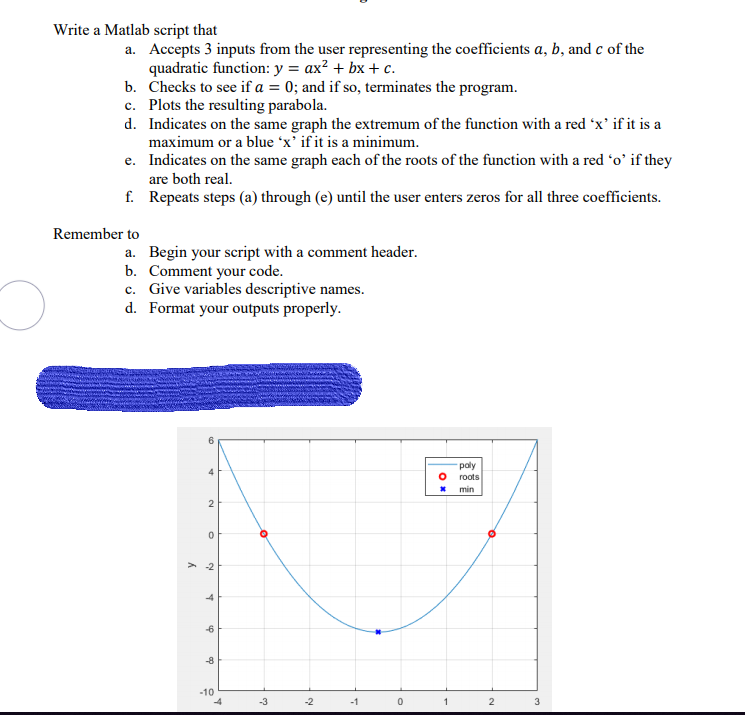
Solved Write A Matlab Script That Accepts 3 Inputs From T Chegg Com

Graphing Y Ax 2 Bx C
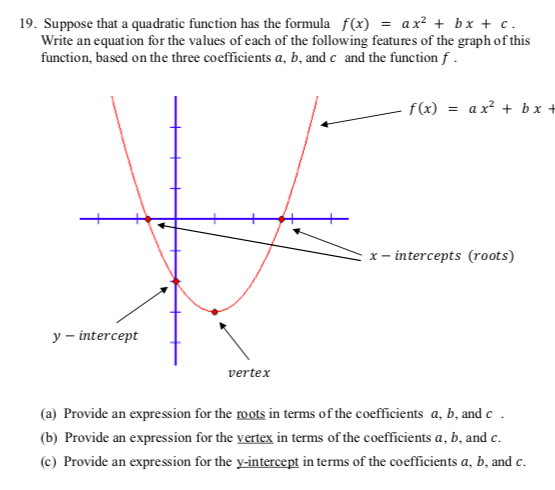
Solved 19 Suppose That A Quadratic Function Has The Form Chegg Com
Q Tbn 3aand9gct66wfxojvmse Jkok7jku0 Hljpvg9iszzzlfoyppxwm1o 03f Usqp Cau

B Value Definition Explanation Video Lesson Transcript Study Com

If The Diagram Given Below Shows The Graph Of Thepolynomial F X Ax 2 Bx C Then
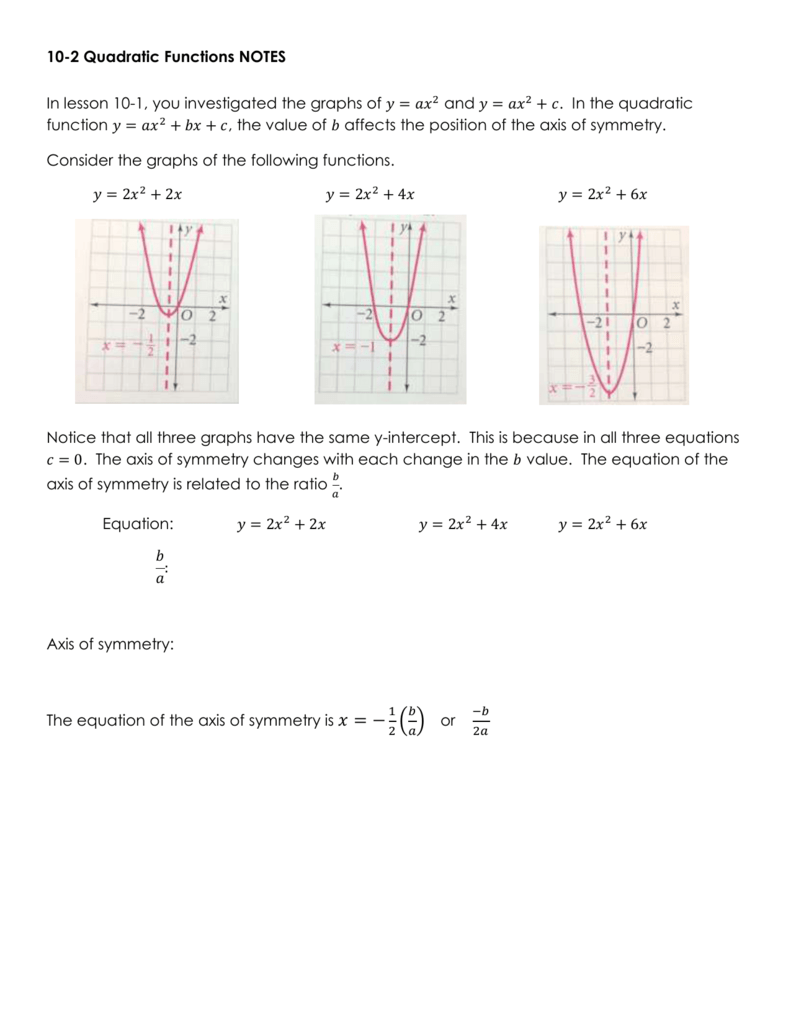
Graph Of A Quadratic Function
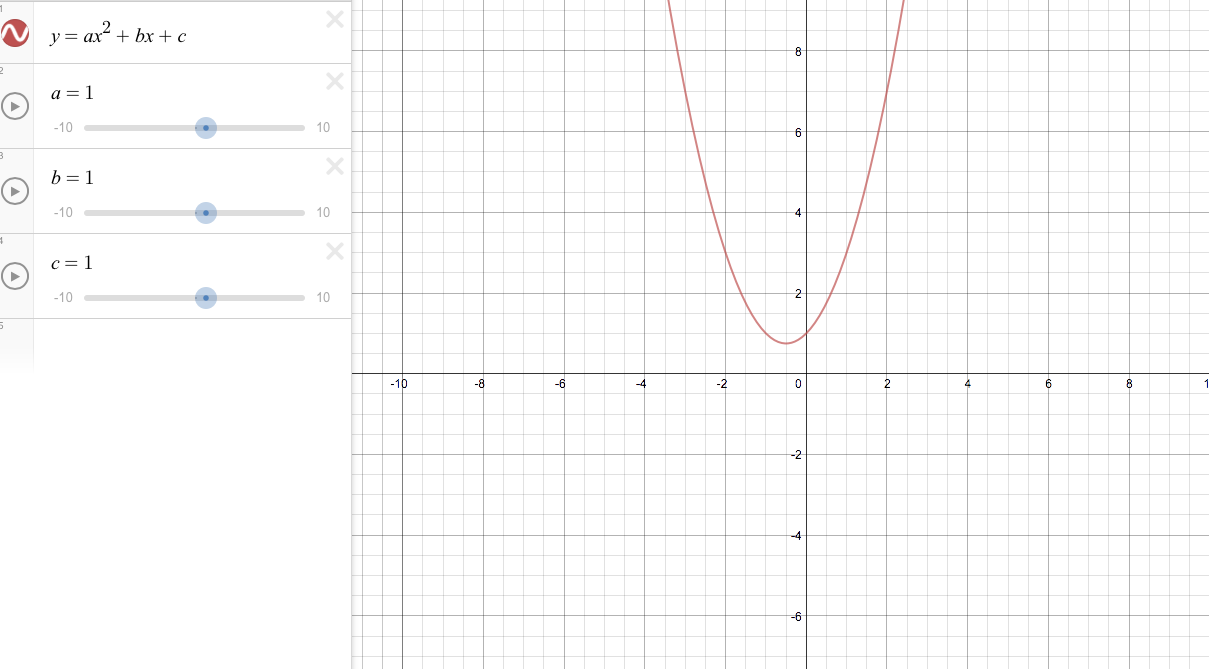
Emat 6680 Class Page For Kursav

The Graph Of The Quadratic Function Y Ax 2 Bx C Is Given Find A B C Brainly Com
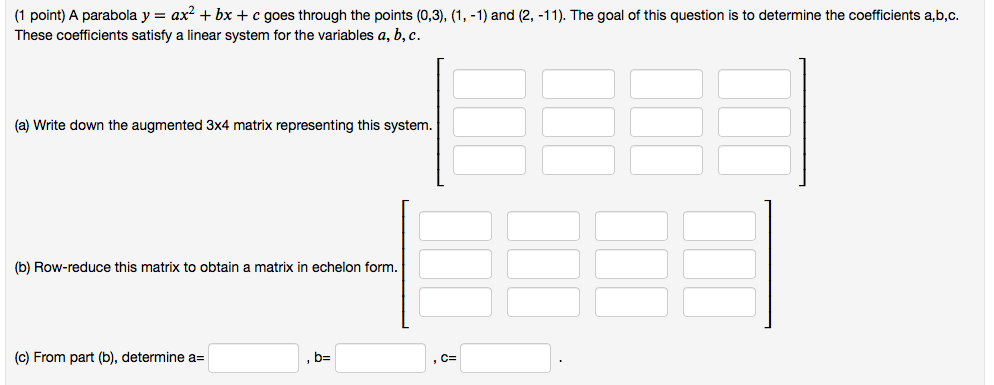
Solved 1 Point A Parabola Y Ax2 Bx C Goes Through Chegg Com

Ch8 Quadratic Equation Solving Methods General Form Of Quadratic Equation Ax 2 Bx C 0 A Quadratic Equation X 2 7x 10 0a B Ppt Download
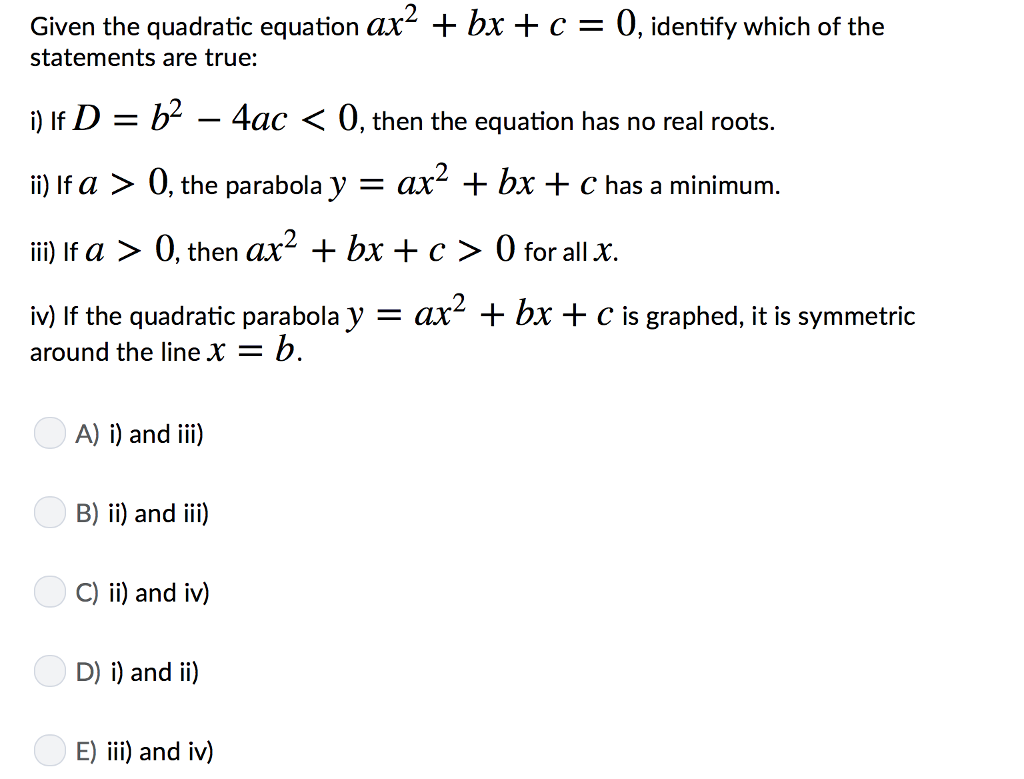
Solved Given The Quadratic Equation Ax2 Bx C 0 Ident Chegg Com
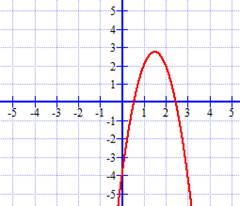
Braingenie Graphing Y Ax Sup 2 Sup Bx C Using A Table Of Values
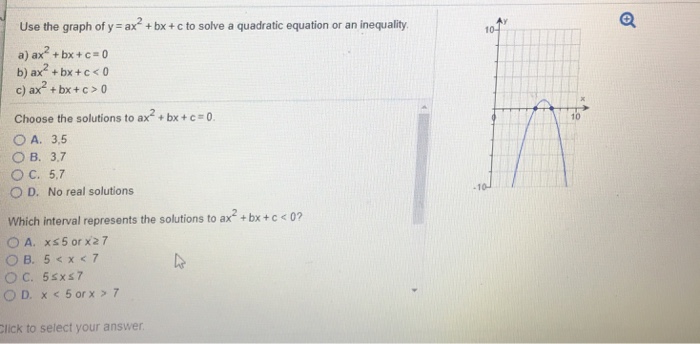
Solved Use The Graph Of Y Ax 2 Bx C To Solve A Quad Chegg Com
Effect Of A B C On Quadratic Youtube
Exploring Parabolas Y Ax 2 Bx C
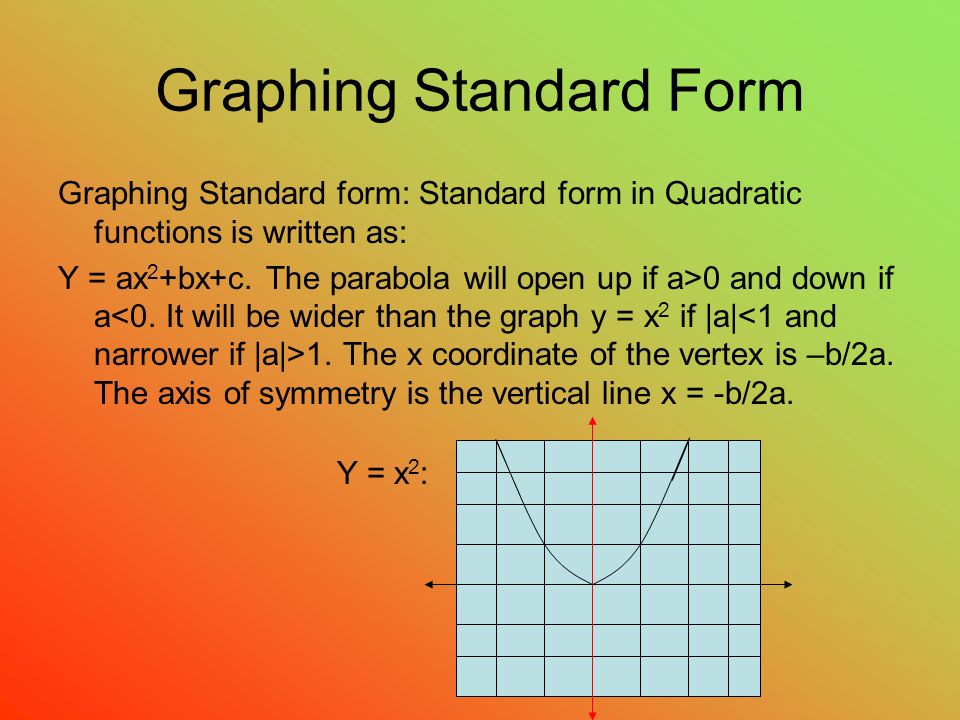
Quadratic Formula Sam Scholten Graphing Standard Form Graphing Standard Form Standard Form In Quadratic Functions Is Written As Y Ax 2 Bx C The Ppt Download
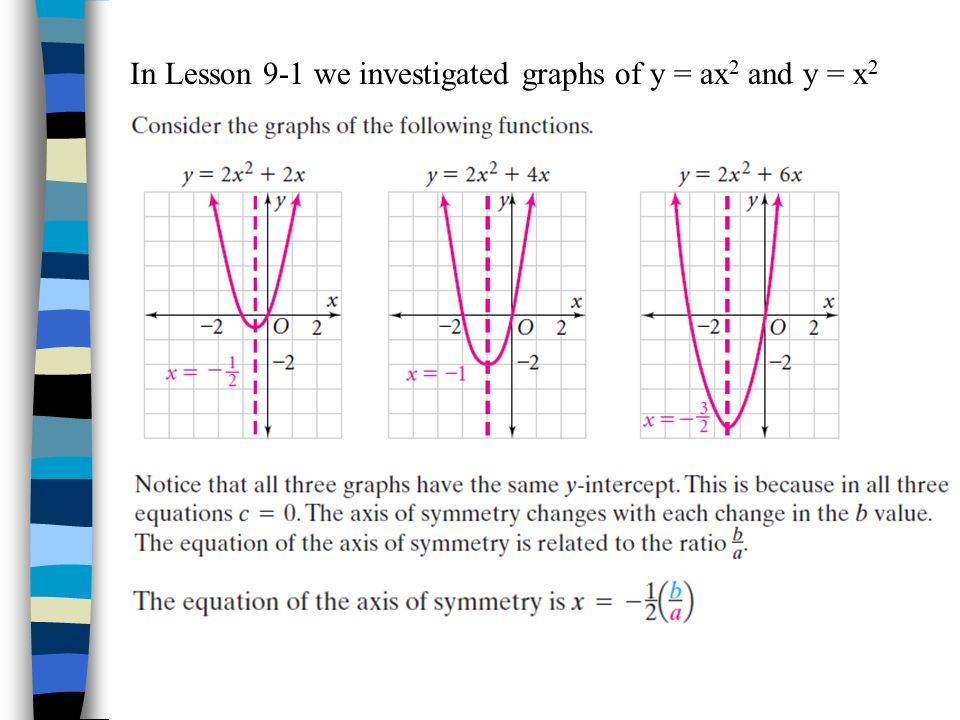
Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download




